مجموع زوایای داخلی مثلث، ۱۸۰ درجه است. این قضیه را به صد روش اثبات کنید. این قضیه را اولین بار دو هزار و پانصد سال قبل، فیلسوفان و ریاضیدانان یونان باستان اثبات کرده اند. البته بعضی میگویند که حتی قبل از آن، ریاضیدانان هندی و بابلی نیز به اثبات این قضیه رسیده بودند. روشهای اثبات آن نیز بسیار مختلف است. اما قدیمیترین جایی که ما اثبات این قضیه را میتوانیم ببینیم، در کتاب اصول اقلیدس است که ۳۰۰ سال قبل از میلاد نوشته شده است.
گفته میشود که پیش از آن، تالس نیز این قضیه را اثبات کرده بود. خواجه نصیرالدین طوسی نیز در کتاب تحریر اصول اقلیدس، اثبات متفاوتی بر این قضیه ارائه میدهد. در ریاضیات مدرن، این قضیه به کمک برخی تبدیلات (transformation) اثبات میشود. شما اگر الان روی یک تکه کاغذ، هر مثلثی بکشید و به کمک نقاله، زوایای داخلی آن را اندازه گیری کنید، مشاهده خواهید کرد که مجموع زوایای داخلی هر مثلثی ۱۸۰ درجه است. وقتی چیزی از طریق ریاضیات اثبات شده است، شما انتظار دیگری هم نمیتوانید داشته باشید. به مدت ۲۳۰۰ سال نیز همه به درستی این قضیه اعتقاد داشتند.
این قضیه یکی از قضایای مهم اصول اقلیدس بود.
حالا یک بادکنک سفید را برداشته و قبل از باد کردن، روی آن یک مثلث بکشید. زوایای داخلی باز هم ۱۸۰ درجه است و باز هم نمیتوانید انتظار دیگری داشته باشید. حالا بادکنک را به یک نفر که نفسش خوب است بدهید تا برایتان باد کند، البته نه آنقدر که در صورتش بترکد. یک بار این اتفاق برای من افتاد و نزدیک بود کور شوم که خوشبختانه نشدم. حالا بعد از باد کردن بادکنک سفید، دوباره زوایای داخلی همان مثلث را اندازه گیری کنید. زوایای داخلی مثلث روی بادکنک باد شده، حالا بیشتر از ۱۸۰ درجه شده است. به شما تبریک میگویم، به هندسهی نااقلیدسی خوش آمدید!
حالا باید برگردیم و هرچیزی که اقلیدس گفته و ما نیز ۲۳۰۰ سال آن را پذیرفتهایم، شک کنیم. مثلا اقلیدس گفته بود و خودش و دیگران اثبات کرده بودند که دو خط موازی هیچگاه به یکدیگر نمیرسند. اما اگر شما دو خیابان موازی مثل نجات اللهی و حافظ را در نظر بگیرید که از جنوب به شمال امتداد یافته اند، این دو خیابان در هیچ نقطهای روی نقشه به یکدیگر نمیرسند. اما اگر بر روی نقشهی کرهی زمین، این دو خیابان را امتداد دهید، در نهایت در قطب شمال و قطب جنوب به هم میرسند. پس دو خط موازی نیز در هندسهی نااقلیدسی میتوانند به یکدیگر برسند.
– اَبا اِباد
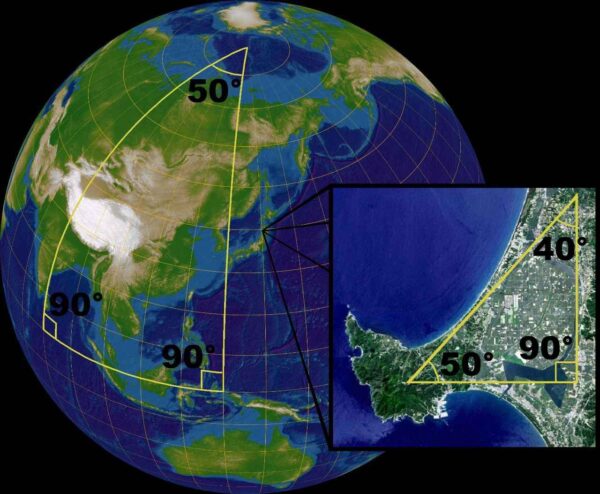
تصویر بالا: همانطور که مشاهده میکنید، مجموع زوایای داخلی مثلثی که روی کرهی زمین رسم شده، ۲۳۰ درجه شده است. شما نمیتوانید چنین مثلثی روی کاغذ رسم کنید که دو زاویهی قائم داشته باشد.