تصویر بالا، نقشهی شهر زیبای کونینگسبرگ (کالینینگراد امروزی) روسیه واقع در غرب این کشور است. البته این شهر، خارج از مرزهای اصلی روسیه قرار داشته و میان لهستان و لیتوانی محاصره شده است. به این شهرها، شهرهای برون بوم گفته میشود. یعنی سرزمینی یا بخشی از یک سرزمین است که کاملاً احاطهشده توسط قلمروی دولت دیگری است. اما در اینجا قصد ندارم به جغرافیای سیاسی و تاریخ این شهر بپردازم. بلکه اینجا قصد من پرداختن به یک مسالهی ریاضیست. در قرن هجدهم، ریاضیدان و همهچیزدان (پالی مث) بزرگ، لئونهارت اویلر وقتی به نقشهی این شهر فکر میکرد، با یک مسالهی ریاضی مواجه شد. همانطور که میبینید، این شهر معماری جالبی دارد. رودخانهای از میان این شهر میگذرد که این شهر را به دو بخش اصلی تقسیم میکند. همچنین داخل این رودخانه و بین دو بخش اصلی شهر، دو جزیره قرار دارد. این دو بخش و همچنین این دو جزیره به کمک هفت پل به یکدیگر متصل شده اند که به هفت پل کونینگسبرگ شهرت دارند. حالا سوال اویلر چه بود؟
اویلر پرسید آیا راهی وجود دارد که بتوان، مسیری را طی کرد، به گونهای که از هر یک از این پلها، فقط و فقط یک بار بگذریم، نه بیشتر و نه کمتر؟
به خاطر همین سوال اویلر بود که این مساله به عنوان مسالهی Seven Bridges of Könningsberg معروف شد. اگر اکنون به این تصویر نگاه میکنید و سعی دارید آن را حل کنید، دو شرط اویلر را نیز مدنظر داشته باشید. شرط اول این بود که غیر از مسیر پلها، مسیر دیگری را برای جابجایی انتخاب نکنید. مثلا یکی نگوید که من به کمک قایق میروم یا اینکه شنا کنم یا منجنیق قرار دهم و با منجنیق بپرم و این مساله را حل کنم. نخیر باید قدم بزنید و فقط مجازید از روی پلها رد شوید نه قایق و پرواز و شنا. حالا کارتان سختتر شد. اما شاید یک نفر به ذهنش برسد که پلی را تا نیمه طی کند.
پس شرط دوم اویلر این بود که اگر وارد پلی شدید، تا ته پل بروید و اینطور نباشد که نصف پل را بروید و برگردید و نصف دیگرش را از سمت دیگر طی کنید. نخیر، دست به مهره بازیست و اگر پایتان را روی پل گذاشتید باید تا آنسوی پل بروید. حالا با در نظر گرفتن این شرط، میتوانید تلاش کنید تا راه حلی برای این مساله پیدا کنید. احتمالا بعد از کمی تلاش متوجه خواهید شد که این مساله جوابی ندارد. اما اویلر ریاضیدان بود نه مهندس. ریاضیدان برخلاف مهندس نمیتواند با سعی و خطا چیزی را اثبات کند و بگوید جوابی ندارد. او باید به صورت ریاضی اثبات کند که این مساله پاسخی ندارد و هیچکس هم نمیتواند پاسخی برای آن پیدا کند. نه اینکه صد راه حل را امتحان کند که جواب نمیدهد، بعد بگوید که پس هیچ راه حلی جواب نمیدهد. او برای اثبات اینکه این مساله جوابی ندارد و برای توضیح اینکه چرا این مساله جوابی ندارد، نیاز به یک زبان ریاضی جدید یا یک فرمالیسم جدید داشت. فرمالیسمی که میتوانست شبکهها را توضیح دهد.
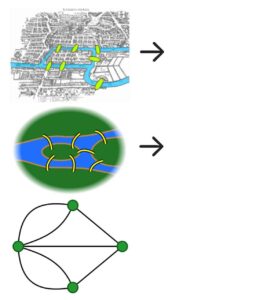
به همین خاطر، اویلر نظریهی گراف را به عنوان یک فرمالیسم جدید اختراع کرد و این مسالهی هفت پل کونینگسبرگ، آغاز نظریهی گراف در تاریخ ریاضیات بود. او به این شکل توانست مساله را به شکل محض درآورد. او هر نقطه را به عنوان یک گره از گراف و هر پل را به عنوان یک گوشه از گراف نشان داد. سپس اثبات کرد که برای اینکه این مساله پاسخی داشته باشد، بایستی فقط صفر یا دو منطقه با تعداد پل فرد وجود داشته باشد. اما در هفت پل کونینگسبرگ، به هر منطقه سه یا پنج پل (با تعداد پل فرد) متصل است و به همین علت، این مساله پاسخی ندارد.

– ابا اباد
