پارادوکس ارنفست

آیا یک پارادوکس مفهومی می‌تواند منجر به یک کشف علمی شود؟

بله مثالش هم پارادوکس ارنفست (Ehrenfest Paradox). پارادوکسی که توانست راه رسیدن به نسبیت عام را به اینشتین نشان دهد و این راه، از طریق هندسه ی غیر اقلیدسی ممکن بود. پائول ارنفست، فیزیکدان اتریشی بود که علاقه‌ی زیادی به کارهای اینشتین نیز داشت. زمانی که البته اینشتین، نظریه‌ی نسبیت خاص خودش را ارائه داد، ارنفست متوجه شد که این نظریه‌ با هندسه‌ی اقلیدسی همخوانی ندارد و به نوعی قابل توجیه نیست.

یکی از خروجی‌های نسبیت خاص اینشتین این است که جسمی که با سرعت بیشتری حرکت می‌کند، دچار یک‌ انقباض در طول می‌شود. مثلا اگر شما دو موشک با طول یکسان داشته باشید و یکی روی زمین باقی بماند و دیگری با سرعتی بسیار بالا و نزدیک به سرعت نور پرتاب شود، کسی که از روی زمین با تلسکوپ به موشکی که پرتاب شده نگاه کند، طول آن را کوتاه‌تر از موشکی که روی زمین ساکن مانده، مشاهده خواهد کرد.

این اتفاق برای شخصی که سوار بر موشک بوده نیز رخ می‌دهد. مثلا اگر قدش دو متر بوده، حالا قدش کوتاه‌تر می‌شود. البته خودش هیچوقت متوجه این موضوع نمی‌شود، چرا که هرچیزی که همراه او در موشک بوده، از جمله متری که بغل دیوار چسبانده تا قدش را با آن اندازه بگیرد نیز کوتاه شده است. فقط دوستانش که از روی زمین او را نگاه می‌کنند، می‌بینند که قدش کوتاه شده است.

تا به اینجای کار با یکی از خروجی‌های نسبیت خاص اینشتین آشنا شدیم. اما این یک تناقض در دل خود دارد. ما از هندسه‌ی اقلیدسی، در مدرسه یاد گرفته ایم که محیط یک دایره را چطور محاسبه کنیم. محیط یک دایره حاصلضرب قطر دایره در عدد پی (۳/۱۴) است. ما از این فرمول بسیار ساده استفاده می‌کنیم و هیچ مشکلی نیز با آن نداریم.

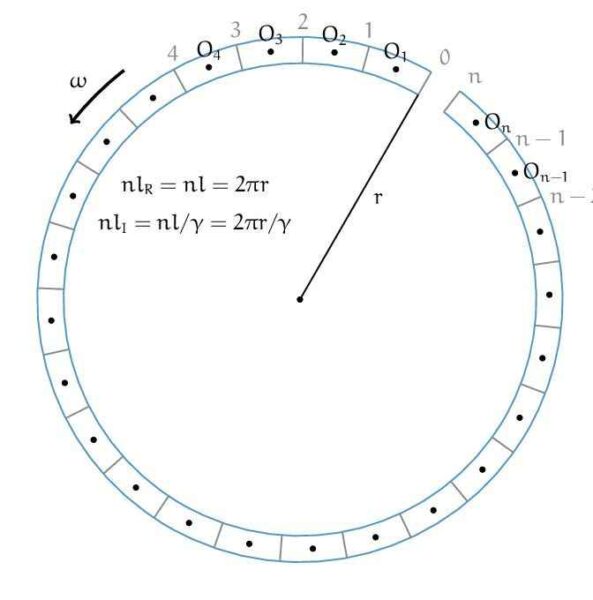
حالا فرض کنید یک حلقه‌ی فلزی دایره‌ای مانند چرخ یک دوچرخه داریم. ما با استفاده از همان رابطه، می‌توانیم محیط این چرخ را محاسبه کنیم. حالا فردی بر دوچرخه نشسته که آنقدر سریع حرکت می‌کند که سرعت هر نقطه‌ روی محیط دایره، به سرعت نور نزدیک می‌شود. حالا طبق نسبیت عام اینشتین، بایستی محیط این دایره دچار یک‌ انقباض شود. در حالیکه قطر این چرخ به همان اندازه دچار انقباض نمی‌شود.

حالا دیگر فرمول قطر ضربدر عدد پی، می‌تواند محیط این چرخ را حساب کند؟

مسلما نه.

آیا این موضوع نشان می‌دهد که نسبیت خاص اشتباه است یا اینکه هندسه‌ی اقلیدسی دیگر اینجا جواب نمی‌دهد؟

اینشتین نشان داد که مورد دوم صحیح است. هندسه‌ای که اینجا جواب می‌دهد، هندسه‌ی ریمانی‌ست که اساسا با هندسه‌ی اقلیدسی تفاوت دارد. وگرنه در این حالت، بایستی مثل شکل، دایره از جایی قطع میشد و محیطش کوتاه می‌شد.

– اَبا اِباد